Trevi drinker

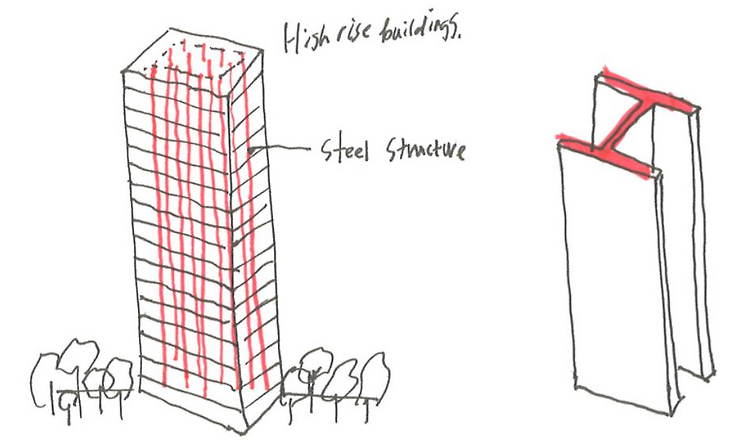
3) Social context and architect's design intention The facade has a strong relationship with society and also its architectural elements where architects' design intentions are strongly revealed. The facade of the building is open to everyone and social understanding is essential. The facade that doesn't fit in with the surrounding buildings, or that looks ugly to people, is the facade that fail..

1) Protection from the external environment The facade is the first membrane where the building meets the outside environment. Protection from the outside environment is the most fundamental requirement associated with the nature of architectural behavior because the original reason for a human to construct buildings is to protect oneself from harsh external environments. So what kind of externa..

The appearance of curtain wall buildings shares the context with the mass production of steel in the 19th century. Since then, steel has rapidly emerged as a new building material. For example. the Eiffel Tower (1889) is a famous building made during this period. Opposition to the Eiffel Tower in the early days was tremendous; however, it is now a symbol of testing the possibility of new buildin..

Column - beam system 1) Composition The origin of masonry architecture was the material. The same is also true for the column-beam architectural system. In areas where this system has developed, wood has been used a lot as a building material. Just like the east Asian countries. There are two basic structural elements in this system. One is a pillar, the other is beams. Pillars are a familiar co..

Masonry system 1) Materials Brick is a very common and popular building material. The brick building is a typical masonry structure. (However, the tall brick buildings that are built today are usually decorative bricks, so we can not call them masonry structures.) Not only bricks but also mud blocks and heavy stones are represented masonry material. Bricks, mud blocks, stones. Let's find out wha..

챕터 06에서는 선분 위의 주어진 점 Q에 대하여 벡터와 변수 t를 이용해 선분 위의 모든 점을 정의했다면, 이번에 다룰 내용은 하나의 선분 위의 주어진 점 Q, P에 대하여 변수 t를 이용해 두 점 사이의 모든 점을 정의하는 것이다. 지난 내용과 변수 t의 범위가 다르니, 여기에 유의해서 내용을 살펴보면 좋겠다. 위의 이미지 처럼 동일한 선분 위에 점 Q와 P 가 놓여있다. 이 두 조건을 가지고 두 점 사이의 모든 점을 정의하는 방법은 벡터 뺄셈 연산을 사용하는 것이다. 앞서 이야기했듯이 벡터 뺄셈은 빼는 순서에 따라서 하나의 점에서 다른 점으로 가는 벡터를 산출해낸다. 따라서 점 Q에서 점 P로 가는 벡터 v는 P - Q로 정의할 수 있다. 이렇게 만들어진 벡터 v의 길이 |v|는, 점 Q에서 P로 ..

챕터 05까지 배웠던 벡터 연산들을 이용해서 3d 모델링 상에서 점과 선을 나타내는 방법에 대해서 알아보려고 한다. 라이노 인터페이스 상에서 3d 모델링을 하면서 선을 긋는 행위는 너무나도 당연하고 쉬운 과정이지만, 이 또한 모두 수학적으로 컴퓨터에 정의되고 있다는 사실을 잊으면 안 된다. 그리고 라이노 상에서 선을 정의하는 데에 벡터가 사용된다. 점, 벡터, 변수 t 를 이용해 선 정의하기 첫 번째로 다룰 내용은 하나의 점과 벡터가 주어진 경우에 변수 t를 이용해서 하나의 선분 위의 모든 점을 나타내는 방법이다. 선분 위의 모든 점을 나타낼 수 있다면, 선이 정의된 것과 다름이 없다. 아래 그래스호퍼 이미지를 통해서 주어진 조건들을 파악해보자. 주어진 정보는 점 Q, 선분의 방향을 나타내는 벡터 v, ..

들어가면서 하중을 구하는 일은 파사드 구조 계산에서 가장 첫 번째로 하는 작업이며 이어지는 모든 계산의 바탕이 되는 작업이다. 특히 파사드에서 절대적으로 중요한 하중은 풍하중이다. 파트 1에서도 얘기가 나왔었지만, 건물이 가볍고 높아지면서 풍하중 이슈가 대두된 것이다. 그렇다면 풍하중은 어떻게 구할 수 있을까? 오늘은 이에 대한 이야기를 해보려고 한다. (1) 코드로 구하는 풍하중 많은 하중과 마찬가지로, 풍하중도 코드에 의거해서 구한다. 여기서 말하는 코드란 building code, 즉 건축법규를 지칭한다. 한국의 경우에는 건축구조설계기준이라는 문서를 통해서 풍하중을 구하는 방법을 명시해두었다. 이 코드는 유럽과 미국 등 국가별로 기준이 다르기 때문에 다른 국가에서는 그에 맞는 계산 식을 사용해 구해..

(1) 벡터 외적의 결과 벡터 외적은 영어로 Vector cross product라고 하며 기호로 ⨯ 를 사용한다. 벡터 외적은 두 벡터 v₁, v₂ 를 재료로 하며 연산의 결과 두 벡터와 법선 (Normal) 벡터 v₃ 가 산출된다. 유의할 점은 벡터 외적 연산에서 순서가 달라지면 반대 방향의 벡터가 나온다는 것이다. v₁ ⨯ v₂ ≠ v₂ ⨯ v₁ v₁ ⨯ v₂ = - (v₂ ⨯ v₁) (2) 벡터 외적의 활용 벡터 외적은 법선 벡터를 사용하는 그 결과 자체로도 그래스호퍼 모델링 시 자주 사용되지만, 두 벡터가 평행한 지 확인하고 싶을 때도 사용된다. 부가적인 활용법에 적용되는 벡터 외적의 특징은 다음과 같다. 두 벡터가 평행한지 확인 서로 평행한 벡터 v₁, v₂ 의 외적 연산 결과는 0이다. 따라..

Building structure system This chapter covers the history of the facade. But Facade's history has an inseparable relationship with the history of the building system. So to understand the history of the facade, firstly, I'm going to talk about the history of the building system, specifically the history of the building methods in a shallow manner. As technology developed, building methods contin..