참고 포스트: https://trevidrinker.com/85
Group point clouds by linear path (1/2)
This project was started while sampling images based on the RGB colour it has. I just intended to pick up the red lines of the input image. However, the task turned out to be more challenging. The reason was that my red colour picker algorithm gave me back
trevidrinker.com
이 포스트는 라이노 그래스호퍼 환경에서 비트맵 이미지에서 커브들을 추출하는 알고리즘 연구의 두 번째 시도이다. 위의 참고포스트는 같은 연구 주제의 첫 번째 시도이다. 그러나 Image tracing 과 관련된 논문을 읽고 난 이후 이 방법은 알고리즘적으로 사용자들의 다양한 코너 케이스들을 해결할 수 없다는 결론에 이르러 과감히 포기하고, 논문에서 읽은 Image tracing 알고리즘을 내 식으로 소화해서 다시 스크립트를 짰다. 참고한 알고리즘은 Peter Selinger 가 제안한 Portrace라는 알고리즘이며, 이에 대한 블로그와 기술문서가 정말 잘 정리되어 있다. 우측 링크 참고. (https://potrace.sourceforge.net/)
1. 알고리즘의 구성
Peter Selinger 의 알고리즘은 크게 다음의 네 단계로 나눌 수 있다.
- 비트맵 이미지에서 배경과 획의 경계를 감지하는 알고리즘이 연속된 비트맵 획을 하나의 닫힌 커브로 만들기
- 1에서 생성된 닫힌 커브를 자연스러운 straigth path segment로 변환하기
- straight path 로 구성된 폴리곤 만들기
- 최종적으로 폴리곤을 bezier curve로 변환하여 원본 비트맵 이미지를 자연스럽게 표현하기
그러나 나는 그래스호퍼 환경에서 다양한 플러그인과 애드온을 사용할 수 있기 때문에 포트레이스의 알고리즘을 완전하게 구현하는 것은 중요하지 않았다. 그 대신, 내가 주목한 것은 1번 비트맵 이미지를 배경과 획으로 구분하는 아이디어, 그리고 1번의 아웃풋을 잘 sorting 해서 그래스호퍼의 polyline이나 interpolate 컴포넌트를 사용하는 것이었다. 정리하자면 나의 cute portrace 알고리즘은 다음의 세 단계로 구성된다.
- 그래스호퍼의 image sampler 을 이용해서 배경 위에 있는 포인트와 획 위에 있는 포인트를 구분하기
- 획 위에 있는 포인트들을 그룹화하고, 그룹내에서 포인트들의 순서를 정렬하기.
- 정리된 포인트 리스트를 interpolate 해서 비트맵 획을 벡터화하기
2. Chunk #1: 배경과 획 구분
배경과 획은 그래스호퍼의 내장 컴포넌트 image sampler를 사용했다. Image sampler는 이미지 위에 행과 열과 배치된 포인트의 rgb 값을 반환한다. 반환된 rgb 값을 이용해서 흰색 rgb(255, 255, 255)는 전체 point list에서 cull을 한다.



3-1. Chunk #2: 포인트 그룹화와 정렬, 함수 mkcr_ptoncrv
가장 핵심은 이곳이다! 만들어진 포인를 어떻게 그룹화하고 정렬할 것인가? 이 부분이 중요한 이유는 우리가 포인트 list를 interpolate 해서 획을 만들어야 하기 때문이다. Gh에서 polyline, interpolate 등 포인트를 input으로 커브를 만드는 컴포넌트는 list에 있는 포인트들의 트리 구조와 트리 내부에서 포인트의 정렬 상태가 매우 중요하다. 왜냐하면 그 순서를 토대로 커브를 만들기 때문이다.
하지만 지금 내가 가지고 있는 포인트 output 은 커브를 생성하는 컴포넌트들을 이용할 수 없는 상태다. Output point list 는 처음에 만든 rectangular grid의 열을 {0}, {1}, {2}... 트리 주소로 하고, 행을 0, 1, 2... 인덱스로 하기 때문이다. 따라서 우리의 목표는 이 리스트를 닫힌 커브로 만들 수 있는 단위를 트리 주소로 하고, 해당 트리 안에서 포인트를 연속적으로 배열해야 한다.

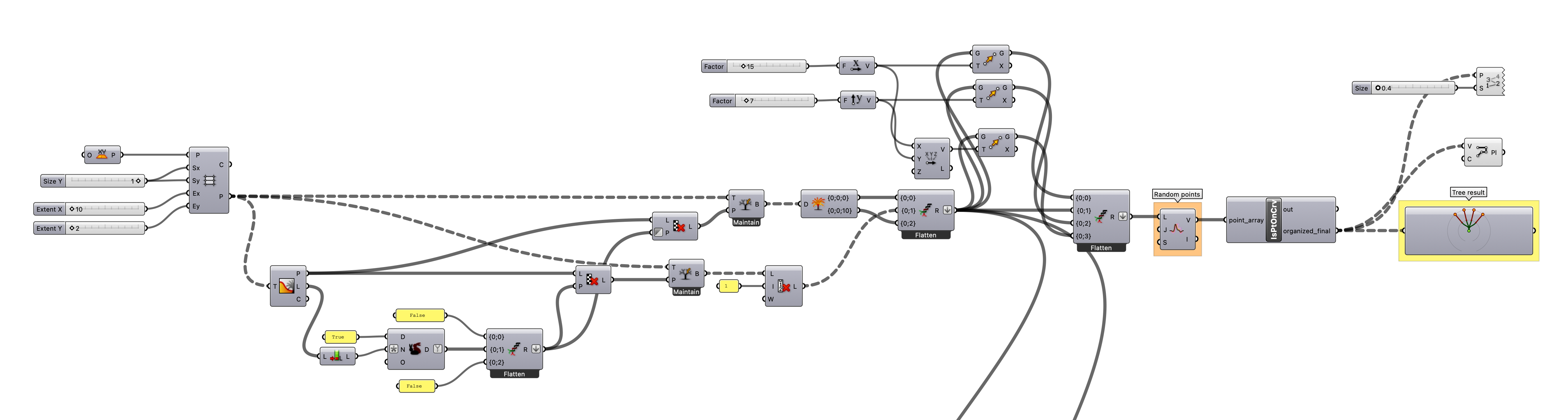
이를 구현하기 위해 Portrace 알고리즘을 참고했다. 간략히, 알고리즘은 왼쪽 하단의 포인트에서부터 계산을 시작한다. 그리고 바로 인접한 포인트를 자신의 바로 뒤 순서에 오도록 리스트에 추가하고, 시작 포인트는 캔버스에서 지워진다. "골라진" 포인트는 또 자신의 바로 옆에 있는 포인트를 계산하고, 그 자신은 또 캔버스에 지운다. 이런 식으로 인접한 포인트들이 점점 캔버스에서 사라진다. 이 루프가 계속되다 보면 어느 순간, 같은 획을 구성하는 마지막 포인트에는 인접한 포인트가 하나도 남지 않게 된다. 그럼 이때 알고리즘은 하나의 닫힌 커브가 완성되었다고 판단하고 트리 주소를 분기한다. 그럼 새로운 트리 주소에서부터 다시 임의의 점이 같은 알고리즘으로 배열된다.
그럼 시작 포인트에서부터 임의의 포인트가 자신에게 바로 인접한 포인트라는 사실은 어떻게 알 수 있을까? 이는 비트맵이 정사각형의 행렬이라는 점에서 착안하여 시작포인트를 중심으로 하고 비트맵의 간격을 반지름으로 하는 원을 그린 뒤, 해당 원 위에 위치한 포인트를 검사했다. 원위에 있는 포인트 t는 시작포인트와 가장 인접한 포인트일 것이다.
import rhinoscriptsyntax as rs
import random
import ghpythonlib.treehelpers as th
def mkcr_ptoncrv(pts, t):
final_list = []
sorted_list = []
while len(pts) != 0:
if t == 0:
circle = rs.AddCircle(pts[0], 5)
sorted_list.append(pts[0])
pts.remove(pts[0])
else:
circle = rs.AddCircle(x, 5)
pts.remove(x)
# Define/ Reset candidates list
candidates = []
# Is point on curve?
for k in range(len(pts)):
isPtOnCrv = rs.IsPointOnCurve(circle, pts[k])
if isPtOnCrv == True:
candidates.append(pts[k])
else:
continue
if len(candidates) == 0:
if len(pts) == 0: # list 의 정말 마지막 point
sorted_list.append(sorted_list[0])
final_list.append(sorted_list)
return final_list
else:
sorted_list.append(sorted_list[0])
final_list.append(sorted_list)
sorted_list = []
t = 0
elif len(candidates) == 1:
x = candidates[0] # candidate 이 오직 1개일 때
sorted_list.append(x)
t = t + 1
else:
x = drct_cmpr(sorted_list, candidates, t) # candidate 이 여려개일 때
sorted_list.append(x)
t = t + 1
# define seqeunce identifier t
t = 0
final_list = mkcr_ptoncrv(point_array, t)
organized_final = th.list_to_tree(final_list, True, source=[0])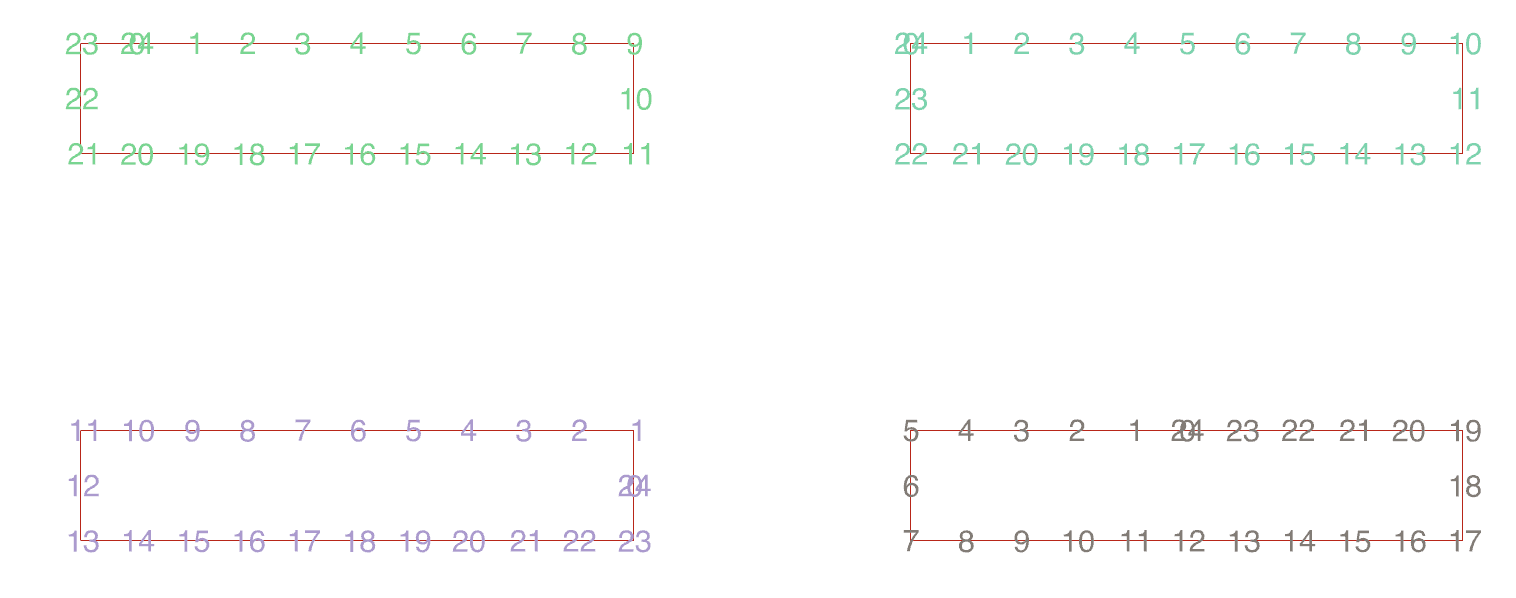
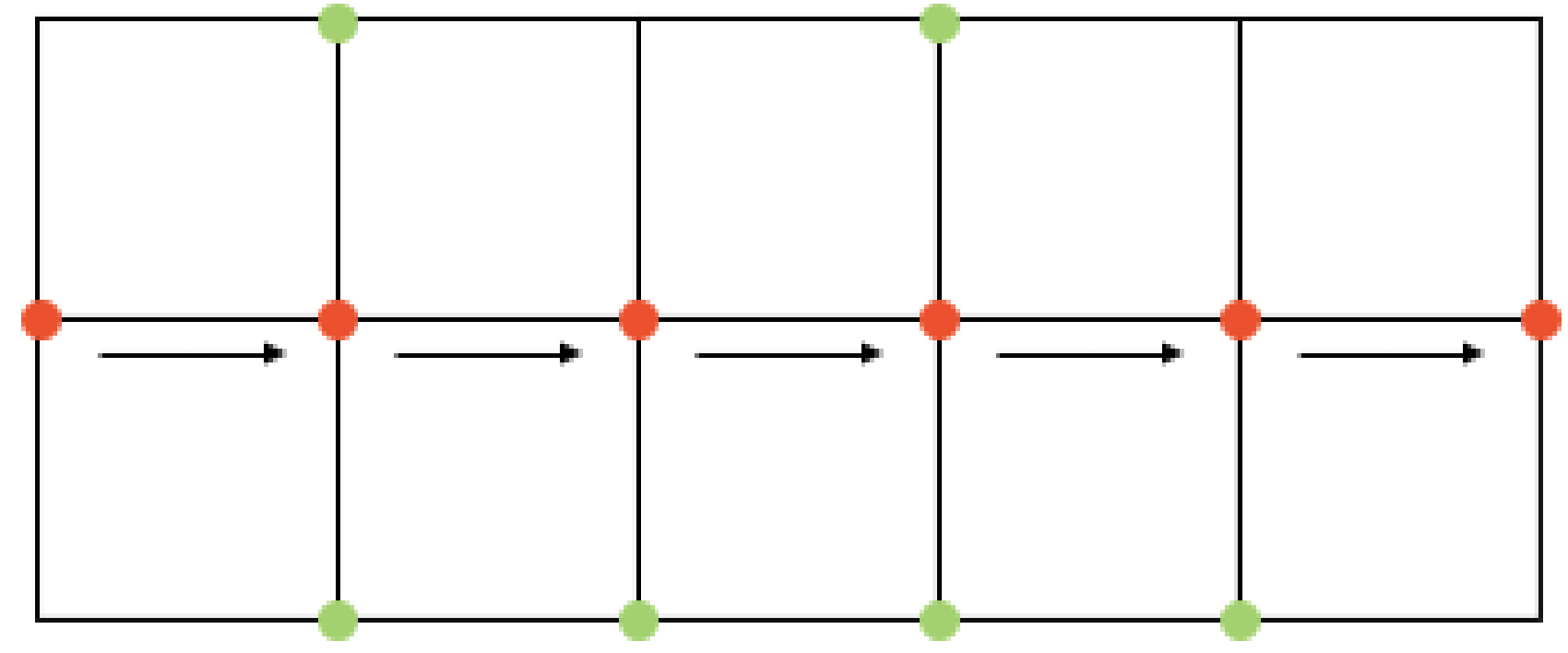
3-2. Chunk #2: 포인트 정렬 시 방향 분석하기, 함수 drct_cmpr
하지만 원 위의 점을 검사하는 것만으로는 포인트들을 제대로 정렬할 수 없다. 왜냐하면, 원 위에 다수의 포인트가 존재할 수 있기 때문이다. 그래서 앞선 mkcr_ptoncrv 함수는 인접한 포인트가 여러 개 일 경우에는 drct_cmpr 함수를 호출한다. 이 함수의 기능은 이미 sorting 된 포인트들의 진행 방향을 분석한다. (direction = rs.VectorSubtract(p2, p1), p2 = sorted_list [-1], p1 = sorted_list [-2]) 그리고 p2와 후보군(candidates_array)에 있는 모든 포인트들 간의 진행 방향을 계산한다. (q = rs.VectorSubtract(i, p2)) 최종적으로 전자의 진행방향과 후자의 진행 방향이 같아지는 포인트 후보군을 sorted_list의 다음 요소로 리턴한다. 최종 후보가 리턴되면 drct_cmpr 함수는 종료되고 진행 중이던 mkcr_ptoncrv 함수가 다시 호출되어 후보를 sorted_list에 append 한다.
def drct_cmpr(sorted_list, candidates_array, indicator):
print "drct_cmpr function is called"
if len(sorted_list) < 2: # reference direction 을 계산할 sorted_list 의 point 가 부족할 때
print "random point was selected"
return random.choice(candidates_array)
else:
p1 = sorted_list[indicator - 1]
p2 = sorted_list[indicator]
direction = rs.VectorSubtract(p2, p1)
for i in candidates_array:
q = rs.VectorSubtract(i, p2)
print(direction, q)
if direction == q: # reference direction 과 일치하는 point 있을 때
print(indicator, 'direction same')
return i
else: # reference direction 과 일치하는 point 없을 때
continue
print "random pt was selected"
return random.choice(candidates_array)4. 코너 케이스의 발견: 포인트 양파
초기 input 이미지로 알고리즘을 돌린 결과를 보여주지 못한 것은 아직 이 알고리즘에 미해결 된 문제가 있기 때문이다. 이 문제를 포인트 양파라고 부르기로 한다. 포인트 양파는 말 그대로 인풋 포인트들이 양파처럼 겹겹이 배열된 상태를 일컫는다. 지금까지 구현된 알고리즘은 1겹의 포인트에서는 잘 작동하지만, 포인트가 겹겹이 이루어진 경우 아웃라인 대한 닫힌 커브를 생성하지 못한다.
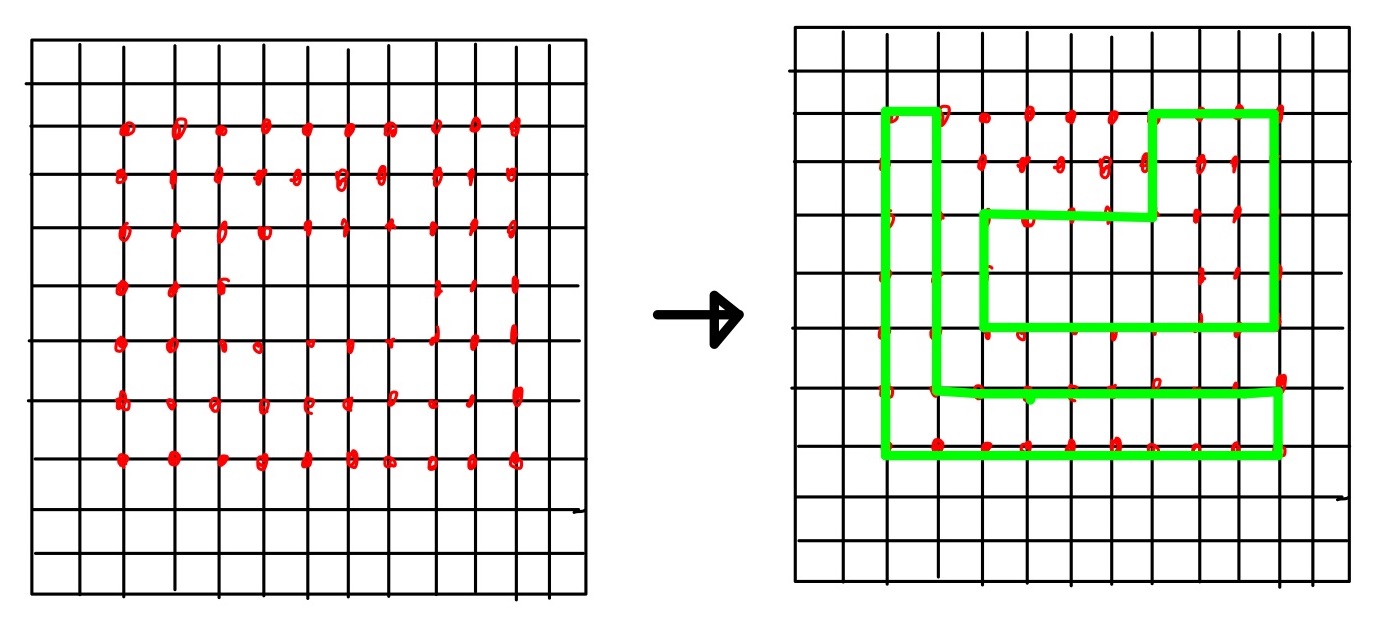
따라서 다음 포스트에서는 이 코너케이스를 해결하여 앞선 인풋 이미지를 커브로 벡터화시키는 작업을 마무리해 본다.
'Python & Coding > Python in Grasshopper' 카테고리의 다른 글
| Sorting 8 cuboid points in Python Grasshopper (0) | 2021.06.20 |
|---|---|
| Dealing with tree structures in Python Grasshopper (0) | 2021.06.18 |
| 라이노 그래스호퍼에서 파이썬 사용하기 (0) | 2021.06.03 |