[FSCM KOR ver.] 파사드 구조 계산 매뉴얼 5.2 단면 성능

 

들어가면서

 

이제, 어떻게 부재를 설계할지 그 모듈을 정했다. 구조 설계 모듈에 따라 세부적인 내용은 다를 테지만, 궁극적으로 비교하는 대상은 아마 외력(P)과 그 외력에 부재가 대항할 수 있는지, 즉 부재의 강성이다. 외력은 정해진 방법으로 구하는 하중일 것이다. 그렇다면 부재의 강성은 어떻게 파악할까? 부재의 강성에 영향을 주는 두 가지 요인이 있는데, 하나는 단면적이 외력에 얼마나 저항할 수 있는지, 단면적과 형상에 따른 단면 성능이고, 또 다른 하나는 재료 자체가 고유하게 가지고 있는 강성의 크기이다.

 

오늘은 그 두 요인중 첫 번째 요인, 부재의 단면 성능을 파악하는 데 사용되는 주요 개념인 단면 2차 모멘트와 단면 계수에 대해서 다뤄본다.

 

(1) 도심

 

 

삼각형의 도심과 무게중심, Centroid and center of gravity in a triangle

 

 

도심은 단면 2차 모멘트를 구할 때 반복적으로 등장하는 개념으로 한번 알아두고 가면 편하다. 개인적으로 단면 2차 모멘트를 이해하면서 가장 헷갈렸던 개념이 도심과 무게 중심의 차이인데, 대부분의 경우 도심과 무게중심은 일치한다고 봐도 무방할 것 같다.

 

영어로 도심은 centroid, 무게 중심은 center of gravity인데 조금 더 풀어서 이해해보자면 도심은 도형의 기하학적 중심, 무게 중심은 도형 무게의 중심 정도가 되겠다. 그러니 물체의 질량이 일정하다면 대개의 경우 도심과 무게 중심은 일치한다.

 

단면 성능을 구할 때의 첫번째 단계는 이 도심을 찾는 과정이 되는데, 도심을 찾는다고 한다면 부재 내에서 단면 1차 모멘트가 0이 되는 지점을 구하면 된다. 

 

(2) 단면 1차 모멘트 VS 단면 2차 모멘트

 

단면 1차 모멘트와 2차 모멘트의 개념은 그 용어부터가 직관적이지 않아서 개인적으로 이해하기가 몹시 어려웠다. 지금까지 이해해본 바를 기술한다면, 이 둘은 본질적으로는 모멘트의 한 형태이며, 따라서 모멘트를 나타내는 수식을 따른다. 그런데 그 수식에 나타나는 차수만이 다른 것이다. 먼저 차수에 대한 얘기를 해보자.

 

- 1차 모멘트 VS 2차 모멘트

모멘트란 부재가 회전이 없는 상태에서 회전하려는 힘이라고 이전 포스트에서 다룬 적이 있다. 모멘트는 힘에 팔 길이(거리)를 곱해서 나타낸다. 이를 식으로 써보자.

M = rⁿ x F (M = 모멘트, r = 거리, F = 힘)     
    If n=1: 1차 모멘트     
    If n=2: 2차 모멘트

 

식에서도 알 수 있듯이 1차 모멘트와 2차 모멘트의 차이는 거리의 차수에 의한 차이라는 것을 알 수 있다. 그렇다면 1차와 2차 앞에 붙는 “단면 모멘트”의 뜻은 무엇일까?

 

- 단면 모멘트

 

앞선 포스트에서 다루었듯이 보에 하중이 가해지면, 보에는 밴딩 모멘트가 발생한다. 발생한 힘 모멘트에 대응하기 위해 부재 내부에서는 역시 응력이 발생하는데, 특히 부재 단면에서 발생하는 응력 모멘트가 단면 모멘트이다. 힘 모멘트가 r(거리)와 F(힘)의 곱으로 나타내어졌다는 걸 떠올려보자. 그럼 단면 모멘트는 어떻게 나타낼 수 있을까?

M = A x D (M = 단면 모멘트, A = 단면적, D = 축에서 도심까지의 거리)

# Note: A는 면적을 나타내는 스칼라 값이고, D는 거리를 나타내는 벡터 값임.

단면 모멘트는 기본적으로 단면이 내는 힘이므로, 모멘트를 표현하는 수식에서 힘 대신에 단면적 A 가 대체되는 값으로 들어간다. 힘 모멘트의 경우 거리와 힘이 모두 벡터 값이었던 반면에 단면 모멘트의 경우 단면적은 스칼라 값, 거리는 벡터 값이라는 게 둘의 차이점이다.

 

(3) 단면 1차 모멘트

 

단면 성능을 구할 때의 첫번째 단계는 도심을 찾는 과정이 되는데, 도심을 찾을 때 사용되는 개념이 단면 1차 모멘트이다. 부재 내에서 단면 1차 모멘트가 0이 되는 지점이 바로 도심이기 때문이다.

 

어떻게 단면 1차 모멘트가 도심의 스토리가 되는지는 수학적인 이야기가 필요하다. 단면 1차 모멘트가 도심을 구하는 개념이라고만 이해해도 충분하지만, 더 궁금하다면 아래 내용을 참고하면 된다.

 

 

위에서 하중이 작용하고 있는 단순 보 입면과 단면 Elevation and section of a simple beam of vertical load

 

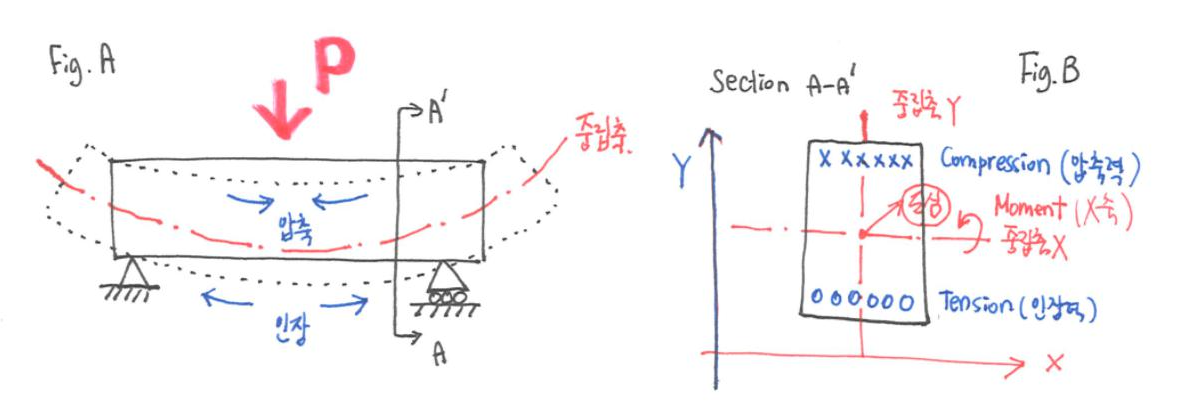
스케치 A와 같은 단순보가 있는데, 하중이 위에서 작용하고 있는 상황을 상상해보자. 그렇다면 하중에 의해 보에는 상부에는 압축력, 하부에는 인장력이 걸리게 된다. 그런데, 스케치에서도 알 수 있듯이 압축력과 인장력이 중간에서 교차되는 지점이 있다. 바로 이 부분을 중립 축이라고 부르며 압축력과 인장력이 모두 0이 되는 지점이다.

 

입면 보의 단면 상황을 살펴보자. 마찬가지로 상부에는 압축력이, 하부에는 인장력이 걸리는데, 압축력과 인장력이 교차되는 지점인 중립축의 교점이 바로 도심이다.

 

M = A x D (M = 단면 모멘트, A = 단면적, D = 축에서 도심까지의 거리)

# Note: A는 면적을 나타내는 스칼라 값이고, D는 거리를 나타내는 벡터 값임.

 

앞서 얘기했던 단면 모멘트를 구하는 식인 M = A x D 를 떠올려 이 보의 모멘트를 구해보자. 우리는 축에서 도심까지의 거리 D를 모르기 때문에 1차 단면 1차 모멘트를 구하기 위해서는 조금 특별한 발상이 필요하다.

 

 

단면 1차 모멘트를 구하는 두 가지 접근 방법 Two approaches aquiring moment of area

 

 

첫 번째 방법은 단면 내부의 미소 면적을 A, 각 미소 면적의 X 축에서의 거리를 Y라고 하는 것이다. 그럼 각 미소 면적에 대한 1차 단면 모멘트는 각 면적과 X 축에서의 거리를 곱한 값이 될 텐데, 이런 미소 면적을 전부 다 더하면 전체 단면적에 대한 1차 단면 모멘트를 구할 수 있을 것이다. 이를 식으로 표현하면 아래와 같다.

 

 

단면 1차 모멘트를 구하는 접근법 #1 Approach #1 calculating Moment of area

 

 

그러나 이 방법으로는 좀 더 나아간 결말을 얻지 못한다. 따라서 두번째두 번째 방법이 등장한다. 두 번째 방법은 단면적을 첫 번째와 같이 작은 미소 사각형으로 나누는 것이 아니라 직사각형의 너비 b를 온전히 갖는 미소 띠로 해석하는 것이다. 이렇게 너비 b와 미소 높이 dy의 미소 띠 면적을 dA라고 하면, 아래와 같은 식이 성립한다.

 

 

단면 1차 모멘트를 구하는 접근법 #2 (X 축) Approach #2 calculating Moment of area (X-axis)

 

 

식을 통해 궁극적으로 Y의 평균 값, 즉 X 축과 도심에서의 거리를 알 수 있었다. 그 결과는 우리의 직관과 일치하는 h/2로 단면 1차 모멘트로 X 축에서의 도심을 알 수 있었다.

 

 

수평 방향으로 하중이 작용하고 있는 단순 보 입면과 3D Elevation and 3D of a simple beam of horizontal load

 

하지만 간과하지 말아야 할 것은 Y 축에서의 모멘트이다. 다음으로 보에 수평 하중이 작용하는 상황을 생각해보자. 단순보를 입면에서 보았을 때 수평 방향의 하중 P가 스케치에서와 같이 가해질 것이다. 이 상황을 입체적으로 파악해보면, 여기서의 보는 Y축에서의 모멘트를 받고 있는 것을 알 수 있다.

 

 

Y 축에서의 단면 1차 모멘트를 구하는 데 적용한 접근법 #2 Approach #2 used in acquiring moment of area in Y axis

 

Y축에 대한 단면 1차 모멘트를 X축에 대한 단면 1차 모멘트를 구했던 것과 같은 방법으로 구해보면, 다음과 같은 식이 성립한다. 결과적으로 X 의 평균값, 즉 Y 축과 도심에서의 거리는 b/2로 역시 우리의 직관과 일치한다.

 

 

 

단면 1차 모멘트를 구하는 접근법 #2 (Y 축) Approach #2 calculating Moment of area (Y-axis)

 

 

(4) 단면 2차 모멘트

 

앞서 단면 1차 모멘트가 도심을 구하는 데 사용되는 개념이라고 했다면, 단면 2차 모멘트는 휨 또는 처짐에 대한 단면의 성능을 예측하는 데 사용되는 단면의 성질을 뜻한다. 영어로는 Moment of Inertia라고 부르기 때문에 대표적으로 I라는 이니셜로 표현된다.

 

 

방향이 서로 다른 두 단면의 단면 모멘트의 합 = 0  Addition of moment of the area with two different direction equals to 0

 

이제 단면 2차 모멘트를 구해보자. 단면 2차 모멘트는 단면의 모멘트를 구하면서 발생하는 뜻하지 않은 오류에 의해 탄생했다. 앞서서 단면 모멘트를 구할 때, A 는 면적으로 스칼라 값이지만, D는 거리롤 벡터 값이라고 했었다. 스케치와 같은 단면을 생각해 볼 때 도심을 기준으로 상부와 하부는 정반대의 방향을 가진다. 즉 압축력을 받는 상부의 단면 모멘트는 AD, 인장력을 받는 하부의 단면 모멘트는 Ax(-D) = -AD이다. 이렇게 각기 구한 단면 모멘트를 구해보면 결과는 0으로 생각지도 못한 일이 발생한다. 분명 단면 모멘트는 힘 모멘트에 대응하여 단면에서 발생하는 모멘트인데, 그 값이 0인 것이다.

 

그래서 사람들은 단면 2차 모멘트라는 개념을 생각해내게 되었다. 합해서 0 이 되는 오류가 방향이 다른 D 에 의해서 발생을 하니, D의 값을 제곱을 시켜주자. D를 제곱하면, 단면 2차 모멘트를 구하는 식은 다음과 같이 된다.

I = Ax(D)² (I = 단면 2차 모멘트, A = 단면적, D = 축에서 도심까지의 거리)

 

 

X 와 Y 축에 대한 단면 2차 모멘트 단면 상황 Sectional circumstances in respectively in X and Y direction acquiring moment of inertia

 

 

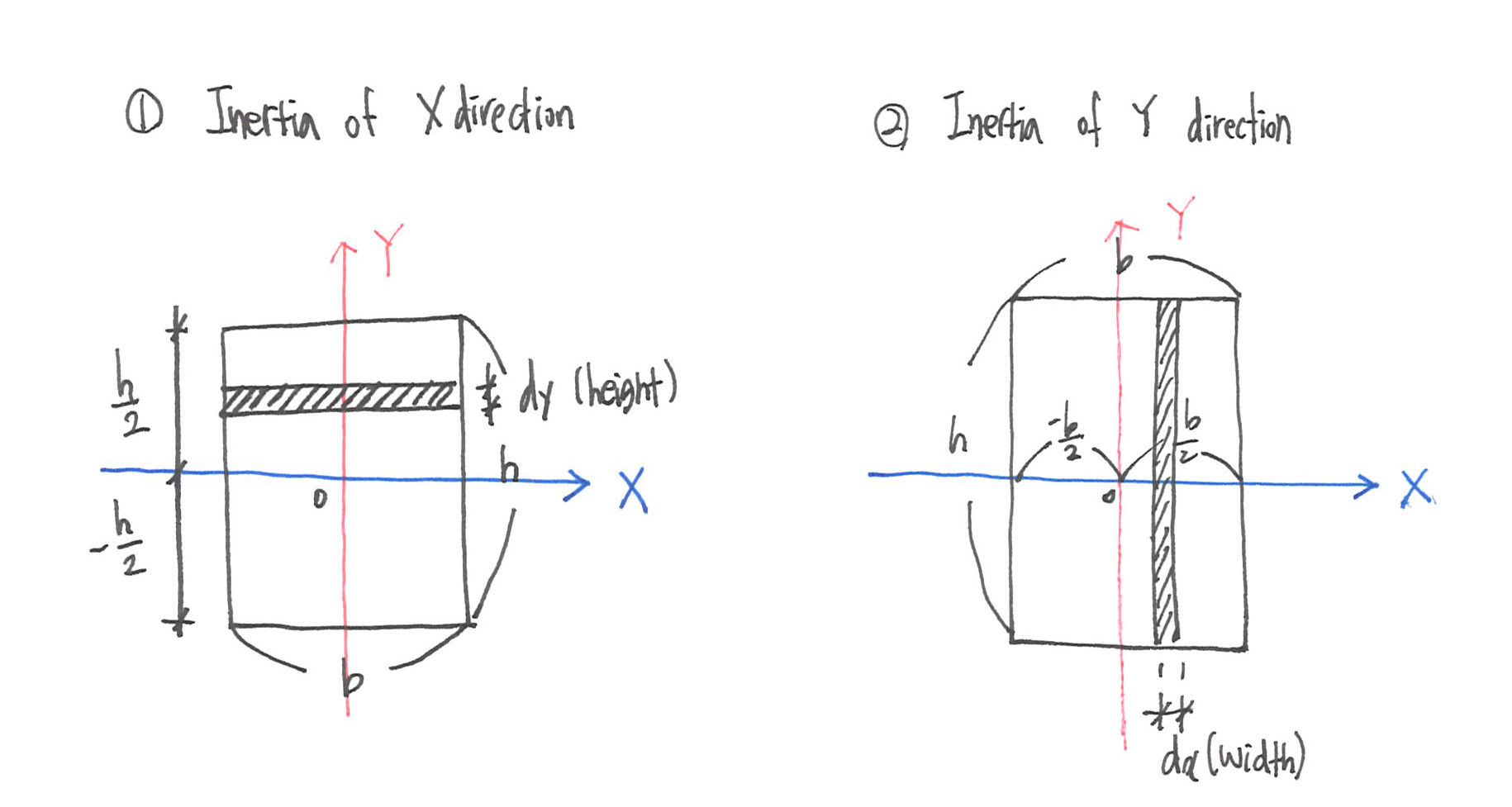
X, Y 축에 대해 단면 1차 모멘트를 구했던 방법과 동일하게 두 축에 대한 단면 2차 모멘트를 구해보면, 아래와 같은 식과 결과가 나온다.

 

 

 

(5) 단면 2차 모멘트의 해석

 

사실 실제 계산 시에는 여러 구조 계산 소프트웨어를 이용해 구조 계산을 하기 때문에 위의 장황한 계산 방법보다 계산해서 나온 이 결과를 어떻게 해석할 것인지가 더 중요한 문제이다.

 

X 와 Y 축에 대한 단면 2차 모멘트의 해석 Comprehensive Moment of Inertia in X and Y-axis

 

스케치 1번과 2번은 각각 X 축과 Y 축을 기준으로 모멘트가 발생하는 상황이다. 1번에서는 수직 하중, 2번에서는 수평 하중이 발생한다. X 방향에 대한 단면 2차 모멘트 결과는 bh3/12로 b에 비례하고, h에는 그 세제곱에 비례한다. 즉 h 가 클수록 단면 모멘트도 압도적으로 커지는 것이다. Y 방향에 대해서도 생각해보자. Y에 대한 단면 2차 모멘트 결과는 b3h/12로 X 축과는 반대로 h에 비례하고, b의 세제곱에 비례한다. b 가 클수록 단면 모멘트가 압도적으로 커진다.

 

그러나 두 경우에 대해서 모멘트가 가해지는 축과 평행한 길이를 가로 길이, 모멘트가 가해지는 축과 수직 되는 길이를 세로 길이라고 한다면, 모두 세로 길이에 대해 단면 모멘트가 세제곱으로 커지는 것으로 정리할 수 있다. 부재 설계 시 기억해야 할 것은, 모멘트가 가해지는 축에 수직 되는 방향의 길이가 길면 길수록 단면 모멘트가 커지고, 단면 성능도 월등히 좋아지는 것이다.

 

(6) 단면 계수

 

단면 계수는 Section of Modulus, 대표 이니셜 Z로 자주 표기된다. 단면계수(Section Modulus, Z)는 도심축에 대한 단면 이차 모멘트를 단면의 가장 끝단에서 도심(centroid)까지의 거리로 나눈 값이다. 단면 계수(Section Modulus, Z)는 도심축에 대한 단면 이차 모멘트를 단면의 가장 끝단에서 도심(centroid)까지의 거리로 나눈 값이다.

 

 

단면 계수 구하는 단순 보 단면 Simple beam section calculating section modulus

Zx₁ = Ix/y₁, Zx₂ = Ix/y₂ (Z = 단면 계수,I = 단면 2차 모멘트)
Zy₁ = Iy/x₁, Zy₂ = Iy/x₂ (Z = 단면 계수,I = 단면 2차 모멘트)

 

단면 2차 모멘트와 단면 계수 모두 단면의 성능을 나타내는 지표이지만, 단면 2차 모멘트가 부재의 처짐을 판별하는 기준이라면, 단면 계수가 활용되는 이유는 부재의 응력을 파악하기 위함이다.

 

 

단면 2차 모멘트가 같은 두 부재에 대한 가정 Assumption of members with same Moment of Inertia

 

단면 2차 모멘트가 같은 두 부재 X와 Y를 생각해보자. 둘의 단면 2차 모멘트는 같지만, 도심에서의 거리가 다르기 때문에 단면 계수는 X 가 Y 보다 작다. (나누는 값이 크기 때문이다) 직관적으로 생각했을 때 둘의 처짐은 같을 수 있겠지만, 깊이가 깊고, 단면적이 작은 X는 Y 보다 부재 내에서 발생하는 응력에는 약하다는 것을 파악할 수 있을 것이다. 

파사드 부재를 설계할때 단면 2차 모멘트로는 처짐의 기준을 만족하는 지를 보고, 이 단면 모멘트를 도심에서의 거리로 나눈 단면 계수가 부재 내에서 발생하는 응력을 감당할 수 있는지도 본다. 즉 단면 2차 모멘트와 단면 계수 이 둘을 함께 만족하는 부재의 단면을 설계해야 한다.

 

나가면서

 

여기까지 구조 계산을 하면서 단면 성능을 파악하는 자료인 단면 2차 모멘트와 단면 계수에 대해서 알아보았다. 파사드 구조 계산의 경우 가는 수직 부재의 풍하중에 대한 휨 모멘트를 구하는 것이 가장 큰 일이기 때문에 두 개념은 파사드 구조 계산에서 정말 빈번히 사용되는 개념이다. 다음 포스트에서는 드디어 개념 파트의 마지막 주인공, 재료의 강성을 나타내는 지표인 탄성 계수와 항복 강도에 대해서 알아보도록 하겠다.