[Computational Engineering] Lecture 1-2. Vector combination

(1) Attitude: All about combinations

Suppose that we have a bunch of vectors(u, v, w ...) and we want to make combinations of them. If we write this process into the equation, that will be like below.

x₁*u + x₂*v + x₃*w (x = scalar)

Making an equation is a nice solution; however, this kind of expression has limits in the case of dealing with huge numbers of combinations. Imagine we have to deal with 1000 vectors and making combinations of them. So this is why we use metrics making a combination of vectors.

 

Then how can we make combinations of vectors using matrices? We only have to know this simple rule:

Vectors go to columns of the matrix.

(2) Independent vector-matrix

Here are given three vectors u, v, and w. To make combinations of vectors, we should put vectors columns of the matrix. As a result, vector u, v, w made matrix A.

 

Making matrix A, we can make combinations of vectors by matrix times vector x. Then the equation will be like below.

Using vector multiplication, Ax will make a combination of matrix A and vector x. Which certainly looks like an upper vector combination equation. ( x₁*u + x₂*v + x₃*w = b) As we can see, the result of the matrix operation was the subtraction of vector x. For this reason, we call matrix A as "Difference matrix", or "First difference matrix".

 

What if we know b and looking for vector x? In this case, we can find x using b. If we define x using b, the result will be like below.

 

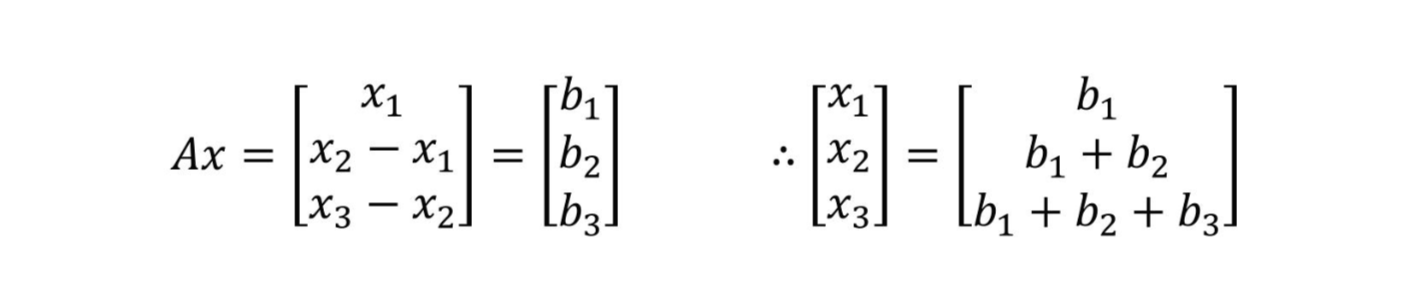
As x1 is b1, in the same manner, x2 and x3 can also be defined by b1, b2, and b3. 

 

Moreover, if we think about the matrix, that results in a matrix combination of b, the result will be the blue matrix above. However, we can notice that the blue matrix is Inverse of A, as it allows us to calculate x.

Through these steps, we found out that the Inverse matrix of A exists, and what it is. However, what's interesting here is that the inverse of A produces the addition of b. (Opposite with matrix A) For this reason, we call matrix A^-1 as "Sum matrix".

 

(3) Meaning of independent vector matrix

We checked out for represented independent vector matrix. Then what's the meaning of these matrices? We found out that in the case of independent vector matrices, all kinds of combinations were possible. For example matrix A, the whole combination can be defined by subtraction of x. This means that combinations of vectors give us (1) the basis of dimensional space, in other words, give us (2) whole dimensional space. Also, it gives us information that whatever vector-matrix it is, (3) the matrix will be invertible.

(4) Dependent vector matrix

Here's another matrix that we can make a comparison with the previous matrix A. Using vector u, v, w below, matrix C was made.

 

The only thing that has changed is the (1,3) component, which changed 1 to -1. In other words, we changed the boundary conditions of matrices. Then let's make combinations of matrix c using vector x. The equation will appear as below.

Intuitively, we can guess that we can not solve this equation. The result value is in a continual loop because its value is defined by one another. Then we can also think that there will be no inverse matrix for C. Let's verify our assumption. In the previous post, lecture 1, if one matrix has an inverse matrix, the only way to make 0 metrics was to multiply 0. When there are other matrices that make 0 matrices means that the matrix is not invertible. Then how about matrix C?

 

If b=0, the equation will appear like above. Cx = 0. Then what's the x that satisfies this equation? Surely, 0 will satisfy the equation. However, not only 0 but numerous other numbers satisfy this equation.

So, our first assumption, that C will be not invertible is verified. Then let's go back to the equation Cx = b. We found out that x₁ - x₃ = b₁, x₂ - x₁ = b₂, x₃ - x₂ = b₃. What happens if we sum all the left side values and right side values?

0 = b₁ + b₂ + b₃

It means that sum of all vector components will end up 0, which we can also check by adding up components of u, v, and w.

 

(4) Meaning of dependent vector matrix

Once again, then what's the meaning of dependent vector matrices? In the case of dependent vectors, we found out that (1) components of vectors end up to 0. This means (2)all vectors are in the same plane and the combination of vectors doesn't (3) produce whole space but sub-space. (In the case of C, sub-space is plane)

 

(5) Summarizing vector space

What are vector spaces? Vector space is a bunch of vectors that takes vectors and are made by combinations of them. From here, we can cover other terms related.

 

• Sub-space: Vector space which is inside of a bigger space
• Whole-space: The biggest sub-space
• In three dimensional space,
  • 0 sub-space: Origin point
  • 1 sub-space: Lines
  • 2 sub-space: Planes
  • 3 sub-space: Whole space

---

* This post is a personal study archive of Professor Gilbert Strang's 18.085 Computational Science and Engineering course at MIT Open Course Ware.
* Please refer to the link below for lecture information.

 

https://youtu.be/C6 pEBqqYnWIocw.mit.edu/courses/mathematics/18-085-computational-science-and-engineering-i-fall-2008/