[라이노 그래스호퍼 벡터] 챕터 08. 벡터로 서페이스 정의하기

지난 두 포스트에서는 변수 t를 이용해서 벡터로 선을 정의하는 방법과, 두 점 사이의 임의의 점을 구하는 방법들을 알아보았다. 이번 포스트에서는 벡터로 surface, 면을 정의하는 방법을 알아보려고 한다.

 

 

(1) 면을 정의하는 방법

 

컴퓨터 상에서 면을 정의하는 방법 중에 하나로, 면 위의 하나의 점을 알고, 그 점에서 면에 대한 법선 벡터(Normal vector)를 알면 면을 정의할 수 있다.

 

하나의 점과 법선 벡터로 면 정의하기 Defining plane with one point and normal vector

 

(2) 벡터 연산으로 면 정의하기

 

벡터 연산만으로 면을 정의하기 위해서는 일직선 상에 놓여있지 않은 서로 다른 점 세 개의 점이라는 준비물이 필요하다.

 

3d 공간상에서의 일직상에 놓여 있지 않은 서로 다른 세개의 점 Three different not lineared points in 3d space

위의 이미지에서처럼 3d 공간상에 일직선상에 놓여 있지 않는 서로 다른 세 개의 점을 그래스호퍼에서 만들었다. 우리의 목표가 하나의 점에서의 법선 벡터를 만드는 것이기 때문에 법선 벡터를 만들기 위한 연산을 거꾸로 생각해보면 벡터 외적 연산을 활용할 수 있다는 것이 떠오른다. 벡터 외적은 서로 일직선상에 놓여 있지 않은 벡터를 두 재료로 받으면, 그 두 벡터에 대한 법선 벡터를 산출했었다. 그렇다면 이렇게 세 점이 주어진 상황에서 어떻게 하면 벡터 외적의 재료인 두 벡터를 구할 수 있을까? 바로 벡터 뺄셈을 이용하면 된다.

 

벡터 뺄셈 Vector subtraction

파란점에서 각각 초록점과 빨간 점으로 가는 벡터를 만들고 싶다면, 점 A에서 점 C의 뺄셈산과 점 B에서 점 C의 뺄셈 연산을 위 그래스호퍼 이미지와 같이 하면 된다. 그럼 그 결과로써 파란 점에서 초록점과 빨간 점으로 가는 벡터가 산출된 것을 볼 수 있다.

 

벡터 외적 Vector cross product

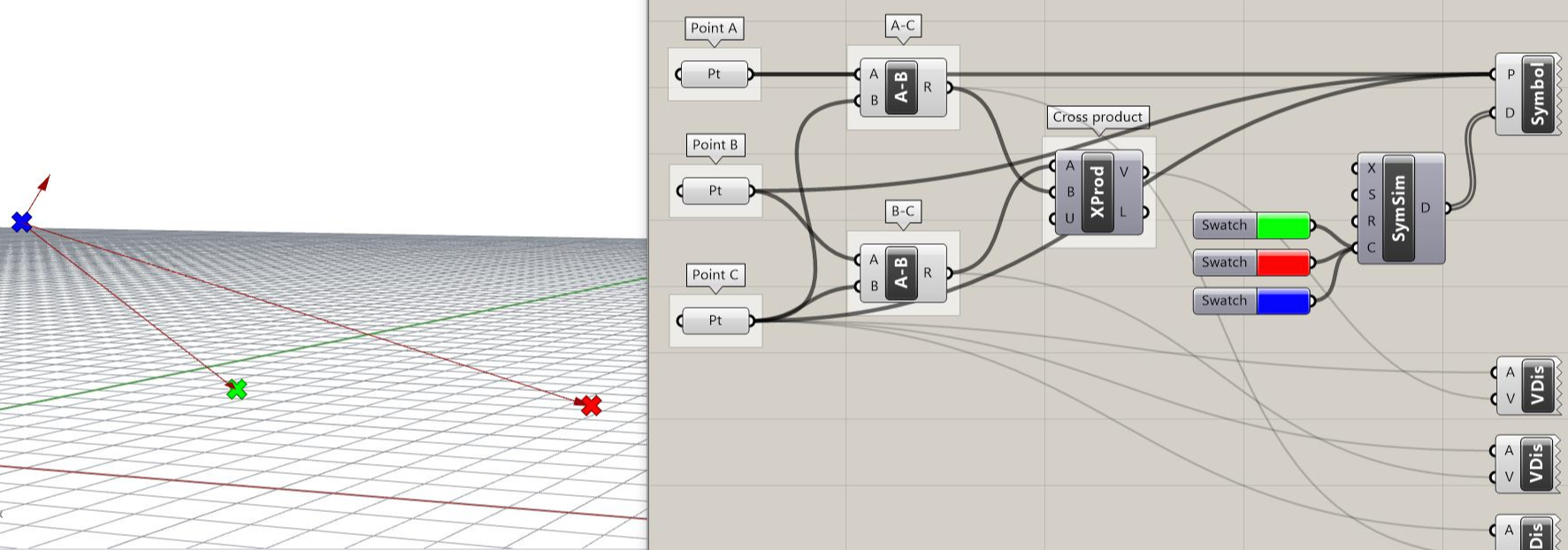
재료가 되었다면 벡터 외적을 통해 법선 벡터를 구하는 것은 쉽다. 그래스호퍼의 벡터 Cross product 컴포넌트를 사용하면 위 이미지처럼 파란 점에서의 법선 벡터가 생긴다. 그럼 이제 면을 정의하기 위한 준비는 전부 끝났다. 

 

법선면 Normal plane

마지막으로 Normal Plane 컴포넌트를 이용하면 벡터 외적 연산을 통해 얻은 법선 벡터와 파란 점을 이용해서 면이 생성된 것을 확인할 수 있다. 

 

(3) 벡터와 면 방정식 정리

 

일직선상에 놓여 있지 않은 서로 다른 세개의 점을 이용해서 법선 벡터 정의하기 Defining normal vector with three non linear points

 

지금까지의 내용을 정리하자면 위 스케치와 같다. 세개의 점 A, B, C를 알 때 한 점에서의 법선 벡터를 구할 수 있고, 그 범선 벡터와 점을 이용해서 결과적으로는 법선 면을 만들 수 있다. 

 

---

* 본 포스트는 Raja Issa의 Essential Mathematics for Computational Design 문서와 유튜브 영상을 참고, 공부하여 작성하였습니다.
* Raja Issa의 영상은 하단 링크를 참고해주세요.

 

https://youtu.be/C6 pEBqqYnWI